How Small is an Arcsecond?
In the motion control industry, accuracy is the difference between target position and actual position. For rotary encoders, we measure accuracy in degrees, arcminutes or arcseconds.

- 1 degree = 1/360th of a circle - used with low accuracy encoders
- arcminute = 1/60th of a degree - used with medium accuracy encoders
- arcsecond = 1/60th of an arcminute - used with high accuracy encoders
Degrees, arcminutes, arcseconds… smaller and smaller units of measurement. So small, they can be hard to visualize.
For this blog post, we thought it would be fun to blow things up! No, not like an explosion—more of an expansion. We'll start off small, then get really big, so we can see what an arcminute and arcsecond would look like in our world, rather than in the small scale of the microelectronics world.
It's All Relative
If someone asks, "How small is an arcsecond?" the answer is relative—it depends on how big the circle is, of which the arcsecond is a part.
For example, encoder disks come in several common sizes, including 1-inch and 2-inch disks. As the disks get smaller, the distance (arclength) spanned by each measurement—degree, arcminute, arcsecond—gets smaller, too. The table below shows arclength distance measured at the outer rim for two disks:
| Measurement | 2-inch Disk | 1-inch Disk | 50.8 mm Disk | 25.4 mm Disk |
|---|---|---|---|---|
| 1 degree | 0.017 inches | 0.009 inches | 0.44 mm | 0.22 mm |
| 1 arcminute | 0.000291 inches | 0.000145 inches | 0.0074 mm | 0.0037 mm |
| 1 arcsecond | 0.000005 inches | 0.000002 inches | 0.00012 mm | 0.000062 mm |
Going in the opposite direction, larger disks have larger circumferences; when you divide them into degrees, arcminutes and arcseconds, those sectors are larger, too.
Let's Go Huge
Let's take a 180 CPR encoder disk, and blow it up—I mean, expand it—so that a single degree measures one foot, or 12 inches in arclength, along the outer rim.
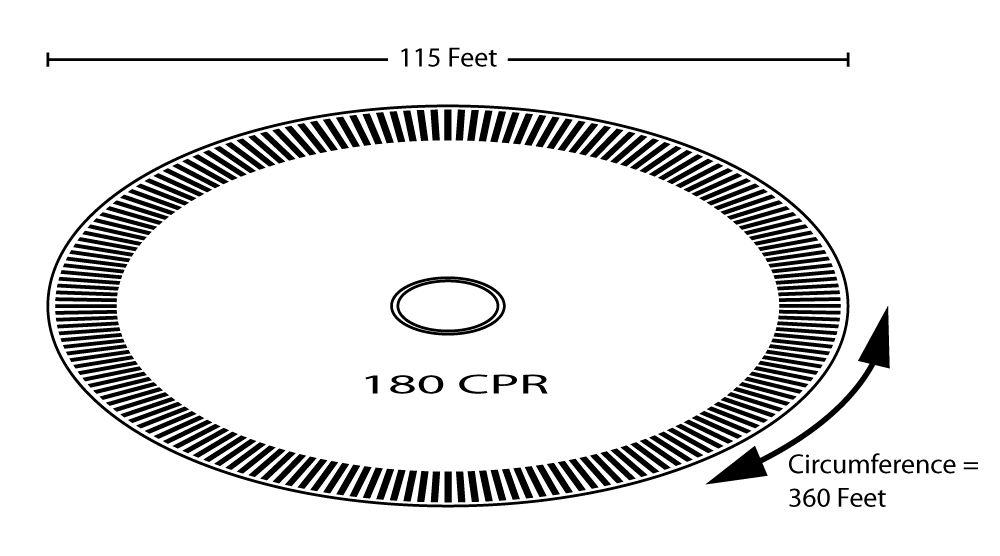
The disk will now have a circumference of 360 feet—one foot for each degree. A 180 CPR disk has 180 lines and 180 windows, for a total of 360; at the rim, each line or window is 12 inches in width.
Which works out great for this blog post, because 360 feet—the circumference of the disk—also happens to be the length of an American football field, including the end zones.
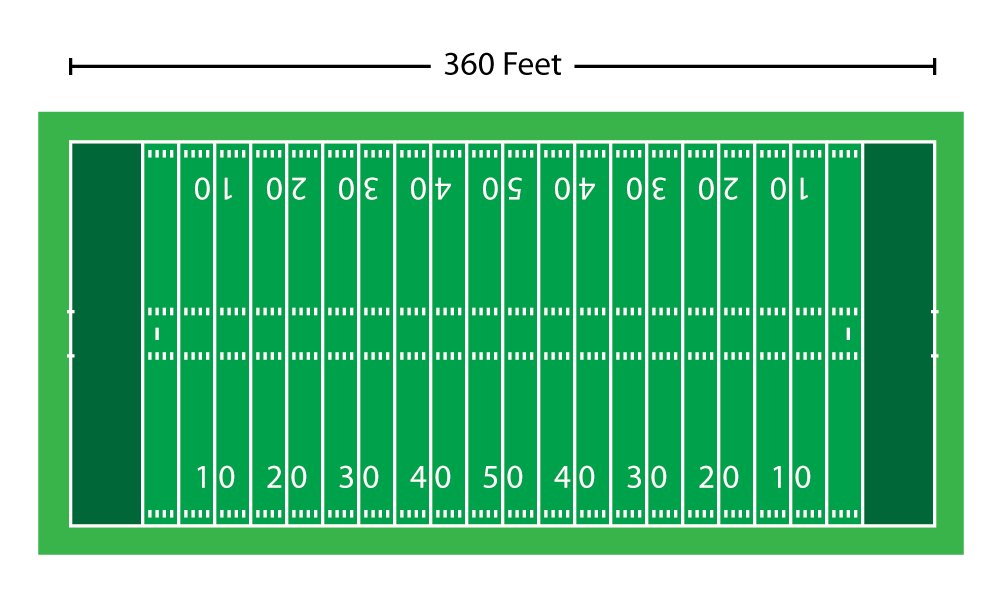
Let's fly our giant encoder disk into a stadium, land it in the middle of the field and make some size comparisons.
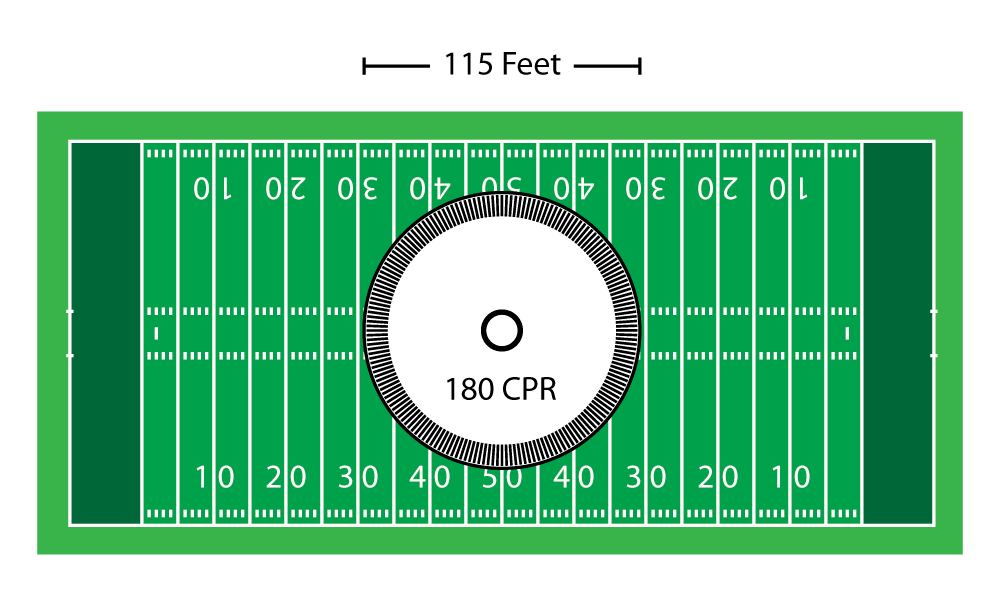
In the drawing below, each foot of the 360-foot-long field matches one degree of the enlarged disk.
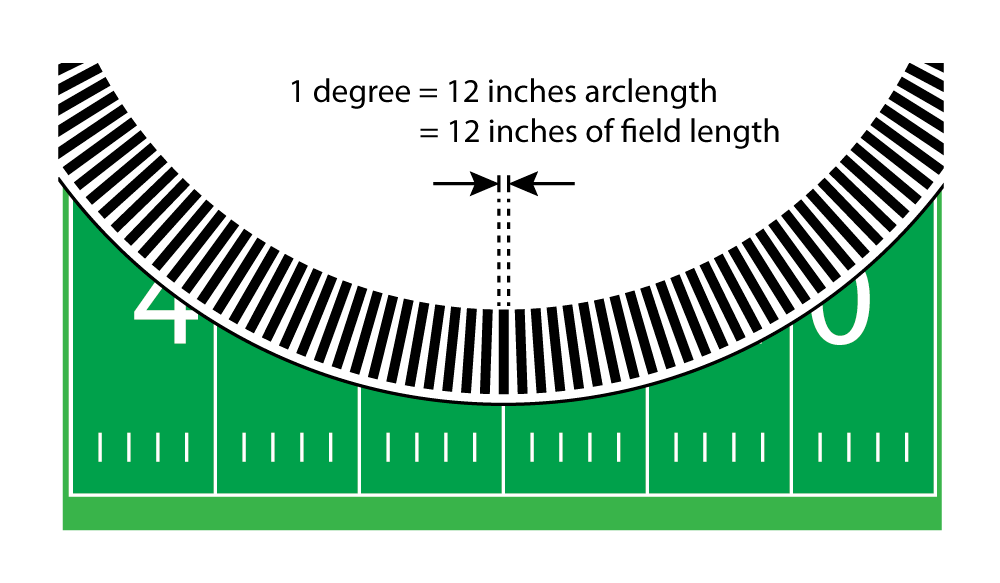
The short white lines on the field, called hash marks, occur every three feet—they match up with three segments on the disk: a line, a window and another line, for example.
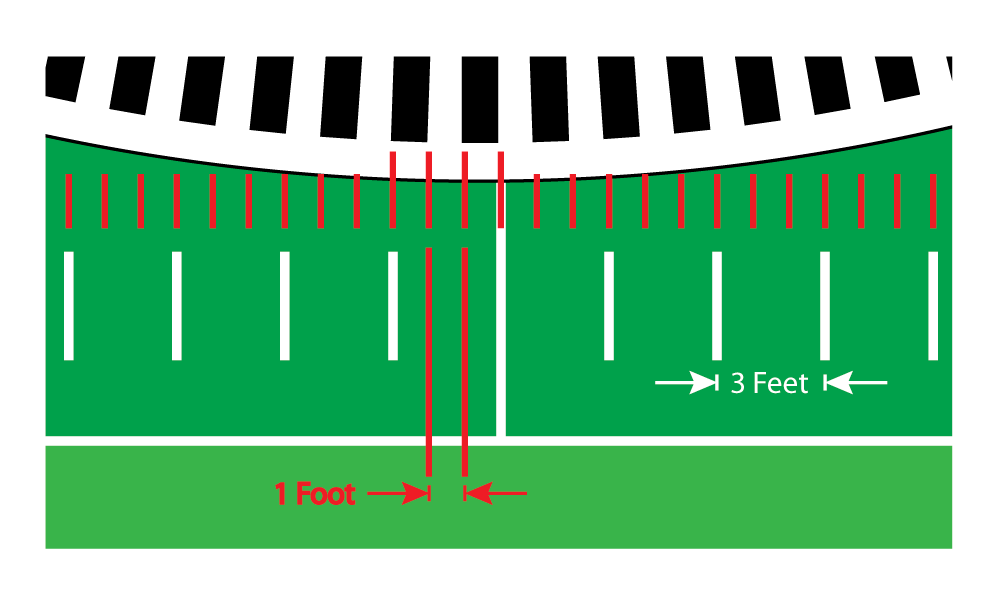
Now let's take that center window—12 inches long—and divide it into 60 equal pieces.
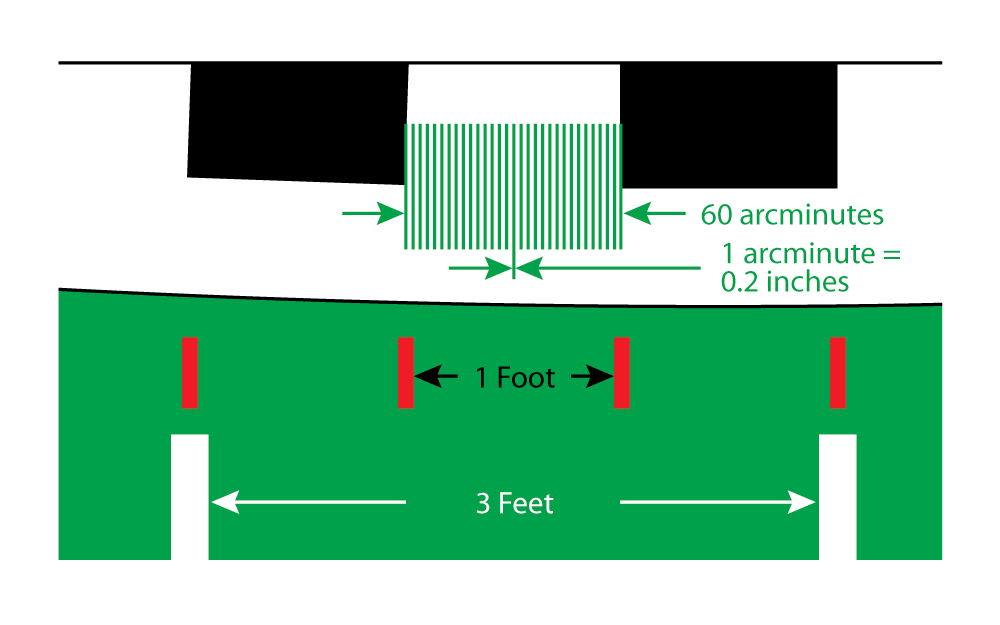
Each one of these new mini-segments would be equal to one arcminute—0.2 inches or about 5mm—literally the size of a pencil eraser.
Divide that pencil eraser—or arcminute—into 60 parts, and you have an arcsecond.
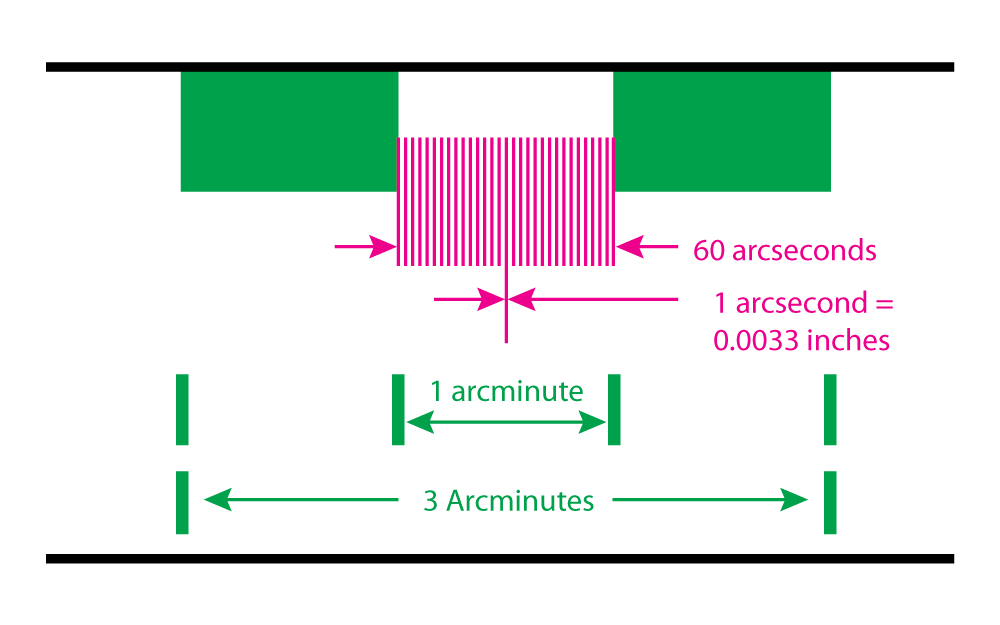
In this case: 0.0033 inches. Just over 3 thousandths of an inch, or 0.083 mm. The thickness of a human hair.
So if you're in the stands at a football game someday, and you happen to notice a pencil slip out from behind a coach's ear and fall onto the sidelines…

…see if you can spot the pencil eraser from where you're sitting.
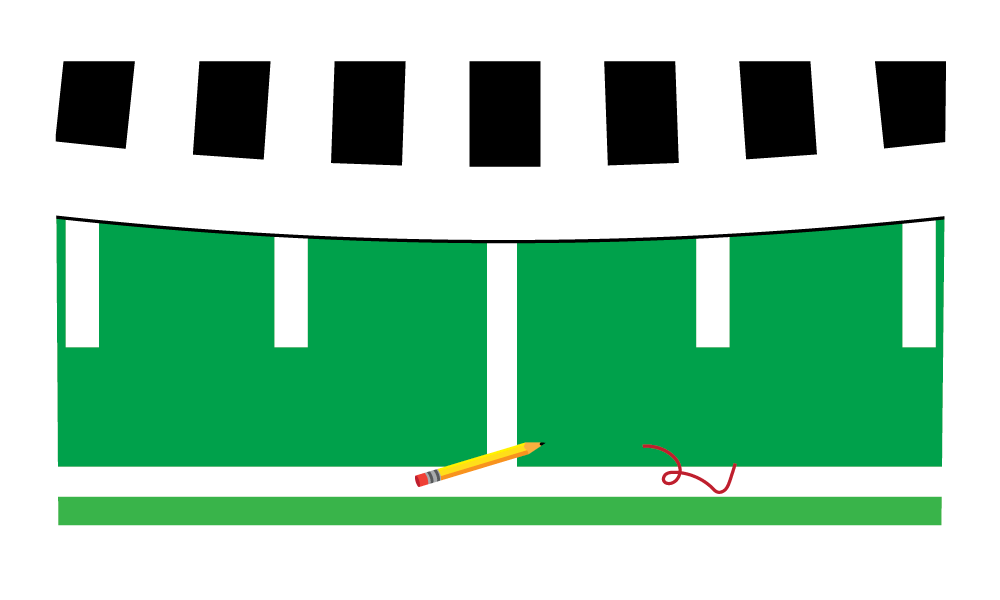
In the huge stadium, that small eraser spans an arcminute. And if there happens to be a hair stuck to that eraser, well—it's the size of an arcsecond. Can you see it? Probably not without some very powerful binoculars; or maybe a telescope.
We hope this example gives you some idea of the relative scale of accuracy that encoders can achieve. A medium accuracy encoder might have accuracy in the range of a tenth of a degree, or 8 – 10 arcminutes—a few pencil erasers in a football stadium. And a high accuracy encoder might measure only a few arcseconds—a few hair-widths, in all of that space.
More in News
Stay up to date
Sign up for our newsletter to stay up to date with our product updates, blog posts, videos and white papers.


